스포츠 베팅의 켈리 기준

베팅이 결실을 맺는 것을 보는 것은 모든 베터의 마음속에 있습니다. 하지만 여러 번의 베팅 실패를 겪은 경험이 한두 번이 아닙니다. 전례 없는 사건의 전환으로 많은 사람들이 과도한 손실로 인해 베팅을 그만두거나 대안을 찾았습니다. 하지만 꼭 그래야만 할까요? 항상 베팅 실패로 인한 후유증에 시달려야 할까요? 대답은 간단할 수 있습니다. 이제 켈리의 기준을 살펴볼 차례입니다.

1956년 J.L. Kelly가 개발한 이 수학 공식은 수년 동안 위험을 최소화하면서 수익을 극대화하는 최고의 대안으로 사용되어 왔습니다. 켈리의 기준은 베터의 돈을 전혀 고려하지 않는 다른 베팅 기준과 달리, 베팅에서 패배하는 것과 전체 자금을 잃는 것 사이의 간극을 메울 수 있는 능력으로 인해 베터들이 선택하는 기준이 되었습니다.

켈리의 공식

켈리의 공식은 사용 가능한 배당률과 당첨 확률을 사용하여 특정 베팅에 자금을 조달하는 데 가장 적합한 금액을 베터에게 안내합니다.

f= (bp - q) / b

B = 소수점 확률 -1
P = 성공 확률
Q = 실패 확률(즉, 1-P)

입력에 대한 자세한 설명

"B"는 특정 베팅 후 획득할 수 있는 전체 금액입니다. "b to 1" 시스템에서는 단순히 명시된 홀수에서 1을 뺀 값으로, 예를 들어 예상 승리 팀이 홀수 @5를 가지고 있고 $10을 베팅하면 +$40을 획득합니다.

"P"는 특정 베팅이 승리할 확률을 의미합니다. 20%의 승리 확률을 가진 팀의 경우, 확률은 0.2가 됩니다.

"Q"는 특정 베팅에서 패배할 확률을 의미합니다. 즉, 승리 확률이 20%인 팀의 경우 같은 팀이 패배할 확률은 80%입니다. 따라서 "Q"는 0.8이 됩니다. 즉, 1 - "P"로 단순화할 수 있습니다.

"F"는 특정 베팅에 자금을 조달하는 데 적절한 금액에 대한 Kelly의 조언입니다.

 

공식 적용

리버풀과 바르셀로나의 승, 무승부, 승리 확률이 각각 2.8, 3.2, 2.4인 두 팀 간의 경기를 예로 들어 보겠습니다. 리버풀이 이길 확률이 251%, 무승부는 401%, FC 바르셀로나가 이길 확률은 351%라고 가정할 때 소수점 이하 10진법을 사용하면 다음과 같이 계산됩니다:

리버풀이 승리합니다: fl [0.25(2.8 - 1) - 0.75] / (2.8 - 1) = - 0.375

게임 추첨: fd [0.4(3.2 - 1) - 0.6] / (3.2 - 1) = 0.1273

바르셀로나 승리: fb [0.35(2.4 - 1) - 0.65] / (2.4 - 1) = - 0.1142

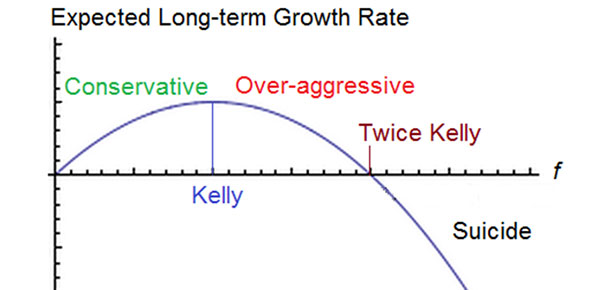
값의 해석

투자자로서 이 베팅에 가장 적합한 옵션은 무승부입니다. 바르셀로나와 리버풀의 승리에 대한 마이너스 값은 두 팀 모두 확실한 승리 가능성이 없음을 의미하므로 베팅할 때 고려하지 않아야 합니다. 위의 수익률로 바르셀로나에 베팅한 경우 11.4%, 리버풀에 베팅한 경우 37.4 %의 손실을 볼 수 있습니다.

 

장점

켈리의 공식은 상당히 이해하기 쉬우며, 베터에게 필요한 것은 팀을 찾고 공식의 데이터를 입력하여 팀에 가장 적절한 금액을 선별하는 것입니다. 이 기준은 또한 잠재적 투자자가 수익을 극대화하는 대신 최소한의 위험을 감수하도록 보장합니다.

단점

이 기준의 핵심은 최대 수익을 추구할 때 최소한의 위험을 보장하는 것이지만, 기준을 사용하는 동안 부적절한 계산으로 인해 실수가 발생하면 계정이 빈곤해질 정도로 비용이 발생할 수 있습니다. 둘째, 베팅은 절대 보장되지 않기 때문에 공식이 한 가지 결과에 많은 베팅을 제안하는 경우 막대한 자금을 잃을 수 있습니다.