2025 年体育博彩的凯利标准

体育投注中的凯利标准 - 每个投注者都希望看到自己的投注结果。但是，他们被迫面对多次投注失败的情况已经不是一次两次了。史无前例的转折让许多人放弃了投注，或因资金损失过大而另谋出路。但事情一定要这样吗？一个人就一定要承受投注失败的反噬吗？答案可能很简单。现在是时候让我们看看体育博彩中的凯利标准了。

该数学公式由 J.L. Kelly 于 1956 年开发，多年来一直是利润最大化而风险最小化的最佳选择。与其他从不为投注者的钱财操心的投注标准不同，凯利标准已成为投注者的首选，因为它有能力弥合输掉一次投注与输掉全部赌注之间的差距。

凯利公式--体育博彩中的凯利标准

凯利公式通过现有赔率和获胜几率，指导投注者为某一投注下注最合适的金额。

f= (bp - q) / b

B = 十进制赔率 -1
P = 成功概率
Q = 故障概率（即 1-P）

对输入的广泛解释

B "是指一个人在特定投注额后可以赢取的全部金额。在 "B 到 1 "系统中，它只是所述的单数减去 1，也就是说，如果推测的获胜球队带有单数 @5，而您下注 $10，那么您将赢得 +$40

P "表示某一投注获胜的可能性。对于胜率为 20% 的球队，概率为 0.2。

Q "是指在某次投注中输掉的概率。也就是说，如果一支球队的获胜概率为 20%，那么同一支球队的输球概率为 80%。因此，"Q "就变成了 0.8。也就是说，它可以简化为 1 - "P"

"F "是 凯利关于适当数量的建议 为某个赌注提供资金。

凯利标准在体育博彩中的应用--公式的应用

以利物浦和巴塞罗那两队的比赛为例，胜、平、胜的赔率分别为 2.8、3.2 和 2.4。考虑到利物浦获胜的概率是 25%，平局的概率是 40%，而巴塞罗那获胜的概率是 35%，使用 "b 到 1 "十进制可以得出以下结果：

利物浦获胜fl [0.25(2.8 - 1) - 0.75] / (2.8 - 1) = - 0.375

游戏抽奖： FD [0.4(3.2 - 1) - 0.6] / (3.2 - 1) = 0.1273

巴萨获胜：FB [0.35(2.4 - 1) - 0.65] / (2.4 - 1) = - 0.1142

数值的解释

作为投资者 这个赌注的最佳选择是平局.巴塞罗那和利物浦的负值意味着这两支球队都没有必胜的把握，投注时不应考虑。根据上述回报率，投注巴塞罗那将损失 11.4%，投注利物浦将损失 37.4 %。

凯利标准专业人员

凯利的公式相当易懂，投注者所需要做的就是寻找球队，并根据公式中的数据筛选出最合适的球队投注额。该标准还能确保潜在投资者在获得最大利润的同时承受最小的风险。

凯利标准的缺点

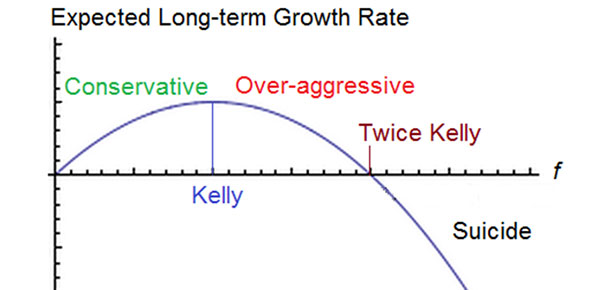
虽然该标准的目的是确保在追逐最大利润的过程中将风险降至最低，但由于在使用该标准时计算不当而导致的错误，可能会使您的资金损失惨重，以至于账户一贫如洗。其次，由于投注永远不会有保证，如果公式建议对某一结果下重注，你就会损失大量资金。

体育博彩使用技巧中的凯利标准

"(《世界人权宣言》) 凯利标准 是有节制的投注者增加赌注的有力工具。通过利用概率和赔率，它可以将风险最小化，将利润最大化。不过，成功与否取决于准确的概率评估和对公式的规范应用。

凯利标准的使用 小贴士

1. 请务必仔细检查您的概率估计值。
2. 即使计算公式建议下大赌注，也要避免将全部赌金的较大部分下注。
3. 将凯利标准与其他投注策略结合使用。