Kelly Criterion in Sports Betting 2025
Kelly Criterion in Sports Betting – it is in the heart of every bettor to see their bets turn into fruition. But not once or twice they have been forced to contend with multiple bet failures. Unprecedented turns of events has seen many quitting betting or seek alternatives due to excessive loss of money. But must things be so? Must one always suffer from a backlash of poor betting? The answer could be simple as it gets. It is about time we take a look at Kelly Criterion in Sports Betting.
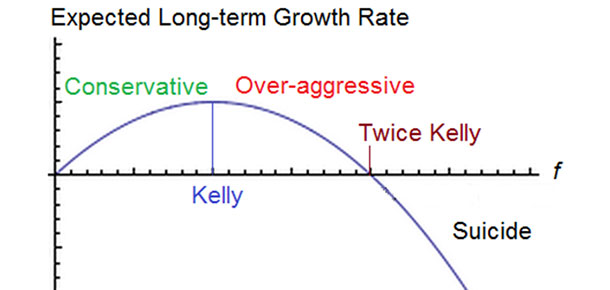
Developed by J.L. Kelly, in 1956, the mathematical formula has over the years served as the best alternative of maximizing profit while minimizing risk. Unlike other betting criteria which never bother on bettors money, Kelly’s criterion have become the bettors choice due to its ability to bridge the gap between losing a bet and losing the entire bankroll.
Table of Contents
Kelly’s Formula – Kelly Criterion in Sports Betting
Kelly’s formula directs a bettor on the most appropriate amount to bankroll a certain bet by using the available odds and the chances of winning.
F= (BP – Q) / B
B = the Decimal odds -1
P = the probability of success
Q = the probability of failure (i.e. 1-P)
Extensive explanation of the inputs
“B” is the entire amount one can win after a particular bankroll. In the “b to 1 ” system it is simply the stated odd less one, that is, if a speculated winning team carries odd @5, and you place a bet of $10, you win +$40
“P” is likelihood of a particular bet winning. For a team having a 20% winning chance, the probability becomes 0.2.
“Q” is the chance of losing in a particular bet. That is, in the case of a team that has winning probability of 20% the same team stands 80% chance of losing. “Q” therefore becomes 0.8. Which means it can be simplified into 1 – “P”
“F” is Kelly’s advice on the appropriate amount to bankroll a particular bet.
Kelly Criterion in Sports Betting – Application of the formula
Take an instance of a match between two teams, say Liverpool and Barcelona with odds of 2.8, 3.2, and 2.4 for win, draw and win respectively. Given that Liverpool’s probability to win is 25%, draw is 40% and that for FC Barcelona winning is 35%, using “b to 1” decimal system it follows that:
Liverpool win: FL [0.25(2.8 – 1) – 0.75] / (2.8 – 1) = – 0.375
Game Draw: FD [0.4(3.2 – 1) – 0.6] / (3.2 – 1) = 0.1273
Barcelona win: FB [0.35(2.4 – 1) – 0.65] / (2.4 – 1) = – 0.1142
Interpretation of the values
As an investor the best option for this bet would be a Draw. The negative value for Barcelona and Liverpool win implies neither of the team has a sure winning potential and should not be considered while betting. With the above returns you stand to lose 11.4% of your stake for bets placed on Barcelona and 37.4 % for bets laid for Liverpool.
Kelly Criterion Pros
Kelly’s formula is fairly comprehensible and all is required from a bettor is to hunt for teams and feed the data in the formula to screen most appropriate amount to wage on a team. The criterion also ensures that a potential investor suffers the least risk at the expense of maximizing profits.
Kelly Criterion Cons
Though the point behind the criterion is to ensure there is minimum risk in the hunt for maximum profits, mistakes arising due to improper computation while using the criterion, may cost ones money to the extent of impoverishing their accounts. Secondly, since bets are never guaranteed, you stand to lose a huge amount of bankroll in the event that the formula proposes heavy betting on one outcome.
Kelly Criterion in Sports Betting Usage Tips
The Kelly Criterion is a powerful tool for disciplined bettors looking to grow their bankroll. By leveraging probabilities and odds, it minimizes risks and maximizes profits. However, success hinges on accurate probability assessments and disciplined application of the formula.
Kelly Criterion Usage Tips:
- Always double check your probability estimates.
- Avoid betting bigger portion of your entire bankroll, even if the formula suggests a high stake.
- Use Kelly Criterion in conjunction with other betting strategies.
Free tips, odds, the best tipsters and advices. Join us and be part of The StakeHunters Community!